Nicole M, Maddie B, Jordan, Shelly, Maddie G, Emma, Nora
Cross Sectional Volumes
A solid figure is generated by rotating a function around an axis.
Volume= ∫A(x) dx
If we find the area for slices perpendicular to the x axis (A(x)), we just need to integrate the area of the slice over the interval [a,b].
Cross Sectional formulas:
Find the area of the cross section and integrate, it is that simple!!
Typically, the area of the cross section is determined through finding the length of one side (top function minus the bottom function).
A dog’s chew toy can be modeled by the region bounded by the function f(x)=2+xcosx and the x-axis over the interval [-2,2] revolved around the x-axis. Find the volume of the solid using circular cross sections.
Step 1: Figure out the formula for the AREA of a circular cross section of this particular graph.
Area= 𝛑(2+xcosx)
Step 2: Integrate over given interval.
Volume= 𝛑 ∫ (2+xcosx) dx
Step 3: Solve.
Volume= 52.43 units
2
2
3
2
-2
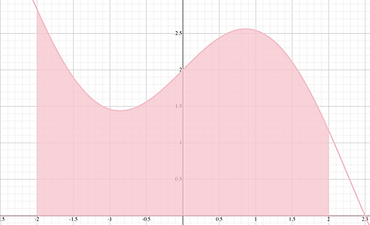

Find the volume of a dog’s bowl using isosceles right triangle cross sections with leg on the base perpendicular to the x-axis. The bowl is modeled by the area bounded by y=2+4sin(x) and y=2+5cos(x) from x=5𝛑 /4 to x=2𝛑.
Step 1:
Area= 1/2((2+5cosx)-(2+4sinx))
Step 2:
Volume= ∫ 1/2((2+5cosx)-(2+4sinx))dx
Step 3:
Volume= 28.02599352 units
2
2
2𝛑
5𝛑 /4
3
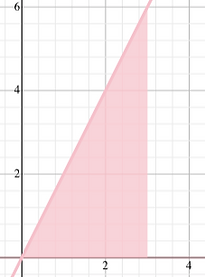
Find the volume of a treat modeled by the function y=2x and the x axis from [0,3] using square cross sections.
Step 1:
A(x)= (2x)
Step 2:
Volume= ∫(2x) dx
Step 3:
Volume= 36 units
2
3
0
2
3