top of page


Nicole M, Maddie B, Jordan, Shelly, Maddie G, Emma, Nora
Ratio Test
Example #1
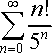
In order to solve this problem, we first need to transfer the sigma notation into the Ratio Test General Formula.
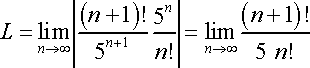
In this step, we condensed the formula by cancelling out some of the repetitive parts of the equation.
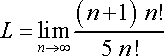
In the condensed problem (above), the '!' next to the '(n+1)' is equivalent to '(n+1)n!'. Since there is an 'n!' in both the numerator and denominator, both 'n!' cancel.
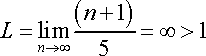
Example #2
Since the problem is completely condensed, it is now acceptable to plug in the value of which the limit is approaching (infinity). In doing so, we obtain the problem '(infinity + 1) / 5'. Ultimately, this equals infinity/5 or just infinity. Infinity is any positive value so we can infer that infinity is greater than one. Based on our rules, any value greater than one causes the problem to diverge.
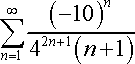
Aforementioned, we first need to transfer the sigma notation into the Ratio Test General Formula.
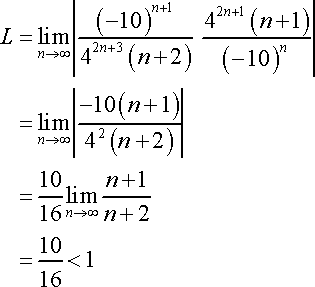
Condense the previous step by cancelling the repetitive parts of the formula.
In this step, we expanded the formula by using the general formula.
Factor out the coefficients and Take the Limit.
By the 'Principle of Dominance', the limit is one. One multiplied by the coefficient is 10/16. Since 10/16 is less than one, the problem converges.
bottom of page